Unidad 3

Unidad 3 - Modelado geometrico

Un mismo objeto puede modelarse de múltiples maneras. La elección del método depende directamente del uso que se le pretenda dar y la elección adecuada es crucial para que el proceso sea eficaz y para evitar problemas innecesarios.

Si se prevé que será necesario hacer cam­bios en los objetos es preferible trabajar con objetos paramétricos y modificadores asocia­dos. Si no es así, la mejor opción es convertir cuanto antes el objeto a malla poligonal y sacar partido de los poderosos recursos de edición de mallas de 3Dstudio para modelar modificando directamente los elementos básicos (subobje­tos): vértices, aristas y caras. Hay que tener presente que, en última instancia, cualquier objeto se convierte en una malla poligonal en el momento de la representación. Trabajar a nivel de malla quiere decir por consiguiente que se tiene el máximo control sobre el resultado y, por añadidura, que se economizan recursos.

La mejor opción, en muchos casos, es tra­bajar inicialmente con objetos paramétricos, grabar el archivo con otro nombre y completar el modelado convirtiendo los objetos a mallas poligonales. De este modo se mantiene abierta la posibilidad de volver al archivo original para sacar partido de los parámetros iniciales de definición del objeto.

La densidad de la malla asociada a un objeto paramétrico se controla desde el momento en que se crea el objeto y puede modificarse en cualquier momento mientras no se lleve a cabo su conversión a malla poligonal. El que se quiera hacer que esta densidad sea mayor dependerá del tipo de objeto (los objetos curvos requieren mayores densidades para simular la curvatura) del tamaño y nivel de detalle requerido y de la distancia de observación o escalas de per­cepción previstas. Hasta tal punto pueden ser cruciales estos últimos aspectos que en muchos casos conviene trabajar en Multirresolución y contar con diferentes copias de un mismo objeto y substituirlas por medio de las opciones que se encuentran en el Panel Utilidades/ Nivel de detalle (Level of Detail, LOD).

Los parches paramétricos o "correctores" y las nurbs son adecuados para generar objetos orgánicos de formas curvas continuas. El nú­mero de caras a que dan lugar es muy alto y, en general, sus ventajas no compensan estos inconvenientes en el caso de la arquitectura excepto en casos especiales. Por esta razón no se incluyen en este curso.

Objetos parámetricos

Formas paramétricas (shapes)

Las entidades básicas, en 3D Studio, como en la mayoría de los programas de modelado, son splines (2D) y mallas poligonales (3D). Pero, al igual que ocurre con las mallas poligonales, las splines no se crean directamente sino que están implícitas en la creación de figuras o formas pa­ramétricas (shapes). Las formas paramétricas disponibles en Max 6.0 son las once siguientes: línea, rectángulo, círculo, elipse, arco, corona, polígono, estrella, texto, hélice (3D) y sección. Son prácticamente las mismas que en versio­nes anteriores.

Su modo de creación y sus parámetros son directos y sobran las explicaciones, excepto, quizás, en el caso de la última que puede re­sultar algo más esquiva. Una sección se crea en relación con un objeto ya existente en la escena. Para probar como funciona esta figura colocarse en un visor de modo que se vea el ob­jeto que se quiere seccionar y con la orientación adecuada. Por ejemplo, si se quiere seccionar verticalmente un cono situarse en un visor frontal o lateral. Desde el Panel Crear/ Formas, presionar el botón Sección y arrastrar: apare­cerá una cuadrícula que representa el plano de corte. Mover y rotar esta cuadrícula de sección hasta que se vea aparecer una línea amarilla sobre el cono que corresponde al corte con el plano. Desde el propio panel o, después, desde el panel de Modificar, presionar el botón Crear


Forma. Se abrirá un cuadro de diálogo en que se pregunta un nombre para la nueva spline que pasará a formar parte de la escena como objeto independiente. Si el botón Actualizar al mover la sección se mantiene activado bastará mover la forma hasta su posición adecuada para que vaya cambiando en función de la sección del objeto de referencia.

Objetos paramétricos generales
En el Panel Crear hay tres grupos de objetos paramétricos: a) Primitivas estándar: Caja, Cono, Esfera, Geoesfera, Cilindro, Tubo, To­roide, Pirámide, Tetera y Plano; b) Primitivas extendidas: Poliedro, Nudo toroide, ChafCaja, ChafCil, Bidón, Cápsula, Huso, Ext-L. Gengon, Ext-C, OndAnillo, Manguera, Prisma; c) Obje­tos AEC (Architecture-Engineering-Construc­tion): Muro, Barandilla, Terreno, Follaje; Puerta pivotante, corredera, plegable; Escalera recta, en L, en U, espiral; Ventana en marquesina, ba­tiente, fija, basculante, corredera, proyectada.







El sistema de creación y modificación de la mayoría de estas primitivas no tiene ningún misterio por lo que tampoco vamos a dedi­carles mucho espacio. Las siguientes notas subrayan algunos aspectos que pueden pasar inadvertidos al comienzo. El siguiente apartado añade algunos comentarios adicionales sobre objetos AEC.

Tener en cuenta que el número de segmen­tos de los objetos es un dato fundamental que afectará tanto a la adición de modificadores, como a su eventual conversión en mallas, como a su comportamiento general. Hay que buscar un punto medio entre la mayor operatividad inherente, en general, a un mayor número de segmentos y el gasto de memoria que supone cada cara adicional innecesaria.

Las esferas cuentan con un parámetro he­misferio que permite especificar un ángulo de recorte horizontal y otro parámetro segmentar que permite especificar un ángulo de recorte vertical. Este mismo parámetro, segmentar, está también disponible en todas las figuras de revolución, cilindros, conos, tubos, etc. En el caso de las esferas, también hay una pequeña casilla que pasa casi inadvertida, "basar en pivote", pero que es útil pues permite conmutar entre crear la esfera a partir de su centro o de su base.

 

3.1 Modelos Geometricos

MODELOS GEOMETRICOS
Describen componentes con propiedades geometricas inherentes y por lo tanto se presentan en forma natural a la representacion grafica. Formas entre los que se puede representar un modelo geometrico:
distribucion espacial y forma de los componentes y otros componentes que afectan a la apariencia de los componentes.
conectividad de los componentes
los valores de datos especificos para la aplicacion

JERARQUIA DE MODELOS GEOMETRICOS

los componentes se usan como bloques basicos para crear entidades de nivel superior, que sirven como bloques para entidades de nivel mas alto. una vez que se descompone una entidad en un conjunto de partes se crean a menudo una jerarquia de dos niveles.

Para simplificar la tarea de contruccion de objetos se usan componentes atomicos especificos: en dos dimencionescomponentes que generalmente se dibujan usando plantillas dibujadad por el computador; en tres dimenciones se usan como bloques basicos, son formas tridimencionales que pueden definirse en funcion de primitivas genericas de nivel mas bajo.

un objeto es una forma compuesta y todos sus datos

una jerarquia se crea para varios propositos:
construir objetos complejos en forma modular empleando invocaciones repetidas a bloques basicos
aumentar la econoomia de almacenamiento
para permitir la propagacion de actualizaciones ya que un cambio en la definicion de un objeto se propaga automaticamente a los objetos de nivel superior.

3.1.1 Modelado de Superficie


Modelo de superficie

Es una versión enriquecida del anterior, puesto que constituye un conjunto de facetas (patches) a partir de los atributos del modelo de malla (lados y aristas), para entregar una representación más completa del objeto. El resultado de cortar un modelo de este tipo por un plano es un conjunto de curvas.

Existen dos enfoques para la presentación de la superficie externa del objeto:

1) El objeto se representa con una lista de facetas, descritas por los lados y las aristas que la delimitan. La lista de caras puede incluir solamente informaciones geométricas propias de cada faceta (tamaño, posición respecto a un origen, etc. ), o puede estar estructurada en un conjunto más complejo, donde los nodos de tipo “cara” se ligan a los nodos arista a través de los nodos “lados”. Estas conexiones pueden presentarse en forma de gráficas o de una estructura de árbol.
2). El objeto se representa empleando superficies de “forma libre”, que el usuario manipula interactivamente a través de puntos llamados de “control”. Se utiliza una superficie representada por ecuaciones paramétricas, que efectúa una aproximación de la envoltura exterior del objeto. Estas ecuaciones paramétricas dan como resultado una malla de elementos finitos de forma específica (generalmente cuadrados o triangulares) y utilizan puntos característicos para cambiar la forma final de la superficie. El modelo algebraico describe un sólido a partir de su frontera. (Conjunto de superficies que separa el sólido de la parte del espacio no ocupada por el).

La frontera se puede ver como la piel del sólido. Obviamente cualquier superficie no determina un sólido. Para que un conjunto de superficies describan un sólido deben satisfacer la siguiente propiedad.

 

3.1.2 Modelado de Solido 

Aquí se representa un sólido mediante el modelo de círculos en movimiento. Los sólidos están constituídos también por partículas en movimiento. La fuerza de atracción entre sus moléculas es muy grande. Cuando las partículas están tan bien ordenadas como las del applet se llaman sólidos cristalinos o cristales. La sal común, NaCl, es un buen ejemplo de cristal.

Los vidrios de las ventanas no están tan bien ordenados, por lo que, en química, no se les llaman cristales sino vidrios o sólidos amorfos.

Al aumentar la temperatura de un cuerpo, aumenta la velocidad de sus partículas.
Cuando su velocidad es suficiente como para que su estructura se desmorone, el sólido se convierte en un líquido: fusión.
Cuando la velocidad es tan grande como para pasar directamente a gas, se llama sublimación.
Cuando la velocidad de las partículas del líquido disminuye, se transforma en un sólido: sodificación.






3.1.3 Procesos Generativos


 

El término generativo se refiere a la imagen que se genera, compone o construye en una manera algorítmica a través del uso de sistemas definidos por un proceso.

Generativo se entiende un proceso creativo que utiliza, se apoya o interactúa con alguna dinámica natural o artificial, orgánica o inorgánica, capaz de generar automáticamente una forma estructurada o un orden estéticamente significativo.

Pero para definirse legitamente generativo, un proceso debe ser determinado y emergente, en el sentido que el orden, la arquitectura y las formas que produce no son determinados de antemano, sino que surgen en el tiempo por la libre interacción entre los elementos del sistema, es decir, materiales, elementos naturales, tecnologías, algoritmos, etcétera.

PROCESOS GENERATIVOS.

se refiere a la imagen que se genera, compone o construye en una manera algorítmica (una a través del uso de sistemas definidos por un proceso.

1a Etapa: Obtención del diseño 3D adecuado

Es muy importante saber cómo dibujar e 3D para adecuar el diseño al sistema que se utiliza para el modelado. El Render elimina todas las caras que se vean por su parte posterior desde el punto de vista actual con el fi de aumentar la velocidad de modelado. El vector normal de las caras; situado en su centro se orienta perpendicularmente hacia el espacio exterior si la cara se dibuja en el sentido anti-horario, esto determina la parte delantera de una cara. Se puede determinar que el Render tome en cuenta las caras traseras para la correcta modelización de objetos que sean transparentes o que estén abiertos y por el punto de vista, se muestre su interior.

La complejidad de un dibujo y su modelado En función de la complejidad del dibujo 3D, número de caras y vértices, se tardarán más o menos en obtener una modelización. Es muy importante establecer u criterio adecuado que relacione la complejidad y el nivel de detalle de cada objeto con su importancia dentro de toda la escena. El estado del dibujo incide en los resultados del modelado Si se da una intersección entre dos caras es posible que se produzca errores según el sistema de modelado utilizado. Las caras coincidentes y coplanares pueden producir resultados ambiguos sobre todo si son de materiales diferentes. Las caras cruzadas o en forma de pajarita también son problemáticas ya que su entorno normal no está correctamente definido 

2ª Etapa: Asignación de materiales.

Contando con el diseño 3D adecuado la segunda etapa debe ser la elección de los materiales para cada objeto. Para ello se dispone de una amplia variedad de los materiales organizados en bibliotecas que el usuario puede aplicar a sus objetos. Los materiales propuestos pueden ser modificados para crear nuevos materiales. En función del material asociado a u objeto puede ser necesario aplicar también unas coordenadas de mapeado.

3ª Etapa: Elaboración de Escenas mediante luces y vistas 3D.

El Render permite la adición de varios tipos de fuentes de luz en torno a los objetos para que estos puedan ser modelados con una mayor apariencia de realismo. Una Escena almacena una vista a elegir entre las que puedan estar previamente creadas, cada escena puede servir para generar las vistas modeladas más representativas del diseño 3D con la iluminación más adecuada en cada etapa. Esta etapa y la anterior pueden intercambiarse.

4ª Etapa: Modelado.

Permite obtener el resultado final directamente en pantalla. Debe seleccionarse la Escena deseada y elegir uno de los tres sistemas modeladores propuestos:

-Modelado Normal.

-Modelado Foto realístico.

-Modelado con Trazado de rayos fotográfico.

Cada modelador establece el grado de acabado, obteniéndose la mayor calidad y realismo con el Trazado de rayos fotográfico y la más rápida y sencilla con el modelado Normal. se deben establecer otros muchos parámetros y condicionantes de modelado que inciden notablemente en el resultado final, tales como: fondo, entorno, niebla, suavizado, sombras, calidad de modelado, resolución, gama de colores, etc.

3.2 Proyecciones 

Las proyecciones transforman puntos en un sistema de coordenadas de dimension n a puntos en un sistema de coordenadas con dimension menor que n. De hecho, drante mucho tiempo se ha usado la graficacion por computador para estudiar objetos n dimensionales por medio de su proyeccion sobre dos dimensiones.


la proyeccion de objets tridimensionales es definida por rayos de proyeccion rectos, llamados proyectores, que emanan de un centro de proyeccion, pasan por cada punto del objeto e intersectan un plano de proyeccion para formar la proyeccion, Por lo general, el centro de proyeccion se encuentra a una distancia finita de plano de proyeccion.








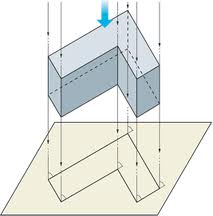
3.2.1 Proyeccion Paralela  


Proyección paralela

Cuando las líneas proyectantes son paralelas –como el anterior objeto alumbrado por la luz del Sol–, se habla de proyección paralela. Es un caso particular de proyección central, donde el foco del haz proyectante estaría a distancia infinita.

El sistema diédrico

Es el caso del sistema diédrico, en el que además se cumple que las líneas proyectantes son perpendiculares (ortogonales) al plano de proyección. En este sistema, a diferencia de los demás, no se obtiene una representación volumétrica del objeto en perspectiva, sino su alzado, planta y perfil. A partir de dichas vistas, se puede conseguir una representación tridimensional del objeto en el sistema axonométrico, cuyas líneas proyectantes pueden ser tanto ortogonales como oblicuas, siendo la perspectiva caballera un caso particular de éste sistema.

El dibujo acotado

Una variante del sistema diédrico, es el dibujo acotado, igualmente de proyección ortogonal, consistente en la representación de alzados o varias secciones paralelas del objeto. Este sistema se emplea para la mejor definición y reproducción de superficies complejas, como son las secciones de un edificio, el casco de un buque, el perfil del terreno y otros elementos similares que, en la práctica, no pueden describirse adecuadamente con los sistemas anteriormente señalados. Son muy utilizados en arquitectura, ingeniería, topografía, etc.








3.2.2 Proyeccion Isometrica

Una de las grandes ventajas del dibujo isométrico es que se puede realizar el dibujo de cualquier modelo sin utilizar ninguna escala especial, ya que las líneas paralelas a los ejes se toman en su verdadera magnitud. Así por ejemplo, el cubo cuando lo dibujamos en forma isométrica queda con todas sus aristas de igual medida.

EJES UTILIZADOS EN EL DIBUJO ISOMÉTRICO. La base del dibujo isométrico es un sistema de tres ejes que se llaman “ejes isométricos” que representan a las tres aristas de un cubo, que forman entre sí ángulos de 120°

a) LÍNEAS ISOMÉTRICAS. Son aquellas líneas que son paralelas a cualquiera de los tres ejes isométricos

b) LÍNEAS NO ISOMÉTRICAS. Son aquellas líneas inclinadas sobre las cuales no se pueden medir distancias verdaderas; estas líneas cuando se encuentran presente en un dibujo isométrico no se hallan ni a lo largo de los ejes ni son paralelas a los mismos. Además las líneas no isométricas se dibujan tomando como puntos de referencia otros puntos pertenecientes a líneas isométricas

MODELOS REALIZADOS EN EL DIBUJO ISOMÉTRICO. Dibujo isométrico de un cuadrado. Dibujo isométrico de una circunferencia. Dibujo isométrico de un arco. Dibujo isométrico de un sólido irregula. (Colaborador del articulo: Wendy castellanos)





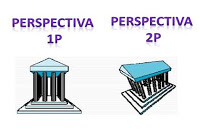
3.2.3 Proyeccion de Perspectiva 

Este tipo de proyección cambia los tamaños de los objetos de modo que aquellos que están mas alejados de la posición de visión se desplieguen de menor tamaño que los que están mas próximos a la posición de visión. Las líneas paralelas sobre la superficie de un objeto se proyectan ahora en líneas que tienden a converger. Los objetos desplegados
como proyecciones en perspectivas parecen más naturales, ya que está es la manera en que el ojo y los lentes de una cámara forman imágenes.

Las técnicas de la proyección perspectiva son generalizaciones de los principios empleados por los artistas al preparar dibujos en perspectiva de objetos y escenas tridimensionales. El plano que la contiene se vuelve el plano de vista. Los dibujos en perspectiva se caracterizan por el acortamiento perspectivo y los puntos de fuga. El acortamiento perspectivo es la ilusión de que los objetos y longitudes parecen más pequeños conforme aumenta su distancia con respecto al centro de proyección. La ilusión de que, cierto conjunto de líneas paralelas parecen unirse en un punto es otra característica de los dibujos en perspectiva. A dichos puntos se les denomina puntos principales de fuga están formados por la intersección aparente de líneas paralelas a uno de los tres ejes principales x, y o z.








3.2.4 Identificacion de Superficies y Lineas Visibles

Es posible aclarar las relaciones de profundidad identificando las líneas visibles. Existe métodos para realizar esto, el método más sencillo es el de resaltar las líneas visibles o mostrarlas de un color diferente otra técnica que se utiliza es muy común para los diseños de ingeniería, que es el despliegue de las áreas no visibles como son las líneas de rayas, uno planteamiento mas consiste en eliminar las líneas ocultas. Pero si se realiza esto, se puede eliminar la información de la forma de la superficie traseras del objeto. Estos métodos mencionados de línea visible también identifican las superficies de los objetos.


Si se debe de desplegar algún objeto con color o con una superficie sombreada se aplican procedimientos de de representación de superficies para las superficies visibles, para que se obscurezcan las superficies ocultas.
Las condiciones de luz se establecen al identificar el color y la ubicación de las fuentes de luz, al igual de definir efectos de iluminación de fondo. Las propiedades de la superficie pueden incluir in formación de la superficie si está trasparente u opaca, al igual si es suave o rugosa.




3.3 Representacion Tridimensional de Objetos

3.3.1 Superficies de Poligonos

a superficie de un polígono se especifica con el conjunto de coordenadas de sus vértices, y parámetros para sus atributos asociados.

Los datos se colocan en tablas que se utilizarán en el procesamiento, despliegue y manipulación de objetos en una escena. Las tablas de datos se organizan en: Tablas geométricas Contienen las coordenadas de vértices y los parámetros para identificar la orientación espacial de las superfices del polígono. Tablas de atributos.Parámetros como grado de transparencia, reflectividad y textura. En cuanto a las tablas geométricas, una organización conveniente para almacenar los datos es crear 3 listas: Vértices Donde se almacenan las coordenadas para cada vértice. AristasContiene apuntadores a la tabla de vértices para identificar los vértices de que se compone cada arista. Polígonos Contiene apuntadores a la tabla de aristas para identificar las aristas de que se compone cada polígono. Además, a los objetos individuales y las caras de polígonos que los componen se les puede asignar identificadores de objeto y de faceta para una referencia rápida.






3.3.2 Lineas y Superficies Curvas

Representación de curvas y superficies

La necesidad de representar curvas y superficies proviene de modelar objetos “from scratch” o representar objetos reales. En este último caso, normalmente no existe un modelo matemático previo del objeto, y el objeto se aproxima con “pedazos” de planos, esferas y otras formas simples de modelar, requiriéndose que los puntos del modelo sean cercanos a los correspondientes puntos del objeto real. Curvas

Representación de curvas

Representación no paramétrica.

La representación no paramétrica de una curva (por ejemplo, en dos dimensiones) puede ser implícita, y = f(x)

o bien explícita,

f(x, y) = 0

La forma implícita no puede ser representada con curvas multivaluadas sobre x (por ejemplo, un círculo), mientras que la forma explícita puede requerir utilizar criterios adicionales para especificar la curva cuando la ecuación tiene más soluciones de las deseadas.

Representación paramétrica.





Una representación paramétrica (por ejemplo, de una curva bidimensional) tiene la forma

P(t) = ( x(t), y(t) )T t1 <= t <= t2

La derivada o vector tangente es

P’(t) = ( x’(t), y’(t) )T

El parámetro t puede reemplazarse mediante operaciones de cambio de variable, y frecuente se normaliza de modo que t1 = 0 y t2 = 1. Aunque geométricamente la curva aparece equivalente, una operación de este tipo normalmente modifica el comportamiento de la curva (esto es visible al comparar sus derivadas).


3.3.3 Superficies Cuadraticas
Definición:

Una superficie cuadrática ( o cuàdrica ) es la gráfica de una ecuación de segundo grado con tres variables x, y, z. La forma general de la ecuación es:

donde A, B, C, …, J son constantes.

1. Elipsoide.

Tiene por ecuación

Las trazas del elipsoide son elipses, es decir, la intersección con planos paralelos a los planos coordenados es una elipse

2. Hiperboloide de una hoja.

Tiene por ecuación

Las trazas del hiperboloide son hiperbolas en planos paralelos al plano XZ y al YZ, mientras que en planos paralelos al XY las trazas son elipses.

El eje por donde se abre el hiperboloide es por el eje cuya variable aparece en la ecuación negativa ( en este caso eje z). La diferencia fundamental entre el hiiperboloide de una hoja y el elipsoide es que tiene una variable con signo negativo.

3. Hiperboloide de dos hojas.

Tiene por ecuación Las trazas de esta superficies son : Para planos paralelos a XZ son hiperbolas al igual que para planos paralelos al YZ.

Se diferencia de las otras superficies ya que tiene dos variables negativas .

4. Paraboloides

Tiene por ecuación Las trazas del paraboloide son: Para planos paralelos al XY son elipses, para planos paralelos al XZ o al YZ son parábolas.

Su diferencia con las otras cuádricas es que tienen una variable que no está elevada al cuadrado, y las otras variables tienen el mismo signo.

5. Paraboloide hiperbólico. Tiene por ecuación

Su diferencia fundamental con las otras superficies es que ella tiene en su ecuación una variable que no está elevada al cuadrado, y las otras variables tienen el signos contrarios.

Trazas:

6. Conos

La superficie cuádrica que tiene por ecuación Se denomina Cono.

Las trazas del cono son:

7. Cilindro circular recto:

Cuando una de las variables x, y o z no aparece en la ecuación de la superficie, Entonces la superficie es un Cilindro. Por ejemplo:

Es un cilindro en el espacio ya que falta la variable z. Por lo tanto, la gráfica del cilindro se extenderá paralelo al eje z

En el plano: En el Espacio:

8. Cilindro circular recto con eje en el eje y : Considere la ecuación:

En el plano: En el Espacio

8. Cilindro parabólico:

Considere la ecuación , que corresponde a una parábola en el plano xy, al variar z se obtiene la superficie

En el plano En el espacio

9. Cilindro elíptico con eje en el eje z:

Considere la ecuación de la elipse en el plano yz , al recorrer el eje x se obtiene la superficie

En el espacio En el plano

10. Cilindro hiperbólico con eje en el eje z:

Considere la ecuación que corresponde a una hipérbola centrada en el ( 0,0) en el plano xy, al recorrer z se obtiene la superficie

En el espacio En el plano

3.3.4 Representaciones de spline

Splines

un spline es una curva definida a trozos mediante polinomios.

En los problemas de interpolación, se utiliza a menudo la interpolación mediante splines porque da lugar a resultados similares requiriendo solamente el uso de polinomios de bajo grado a la vez que se evitan las oscilaciones, que en la mayoría de las aplicaciones resultan indeseables, que aparecen al interpolar mediante polinomios de grado elevado.

Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas. La simplicidad de la representación y la facilidad de cómputo de los splines los hacen populares para la representación de curvas en informática, particularmente en el terreno de los gráficos Splines Durante el proceso de diseño de edificios, automóviles o aviones, las formas finales de los objetos se modelaban a tamaño real (o casi real) donde las curvas se representaban usando splines, largas tiras de plástico o metal moldeadas por pesos ubicados en posiciones específicas. Matemáticamente, estas curvas pueden ser descritas por la unión de secciones de polinomiales cúbicas cuyas primera y segunda derivadas son continuas entre cada sección de la curva.

En Computación Gráfica, una spline es comúnmente referida como una curva compuesta de secciones polinomiales satisfaciendo ciertas condiciones de continuidad entre ellas. Representaremos una curva polinomial cúbica en su forma paramétrica P(t) = B1t3 + B2t2 + B3t + B4 t1 <= t <= t2 Una spline es descrita por un conjunto de puntos llamados puntos de control. Cuando la spline contiene todos los puntos de control se dice que la curva interpola los puntos. Cuando lo anterior no es cierto, se dice que la curva aproxima los puntos. Mientras que el primer tipo de spline es particularmente útil en procesos de digitalización de datos y especificación de trayectos para animación, el segundo es principalmente usado en herramientas de diseño para estructurar superficies de objetos.

Durante el proceso de diseño de edificios, automóviles o aviones, las formas finales de los objetos se modelaban a tamaño real (o casi real) donde las curvas se representaban usando splines, largas tiras de plástico o metal moldeadas por pesos ubicados en posiciones específicas. Matemáticamente, estas curvas pueden ser descritas por la unión de secciones de polinomiales cúbicas cuyas primera y segunda derivadas son continuas entre cada sección de la curva.

En Computación Gráfica, una spline es comúnmente referida como una curva compuesta de secciones polinomiales satisfaciendo ciertas condiciones de continuidad entre ellas.

Representaremos una curva polinomial cúbica en su forma paramétrica

P(t) = B1t3 + B2t2 + B3t + B4 t1 <= t <= t2

Una spline es descrita por un conjunto de puntos llamados puntos de control. Cuando la spline contiene todos los puntos de control se dice que la curva interpola los puntos. Cuando lo anterior no es cierto, se dice que la curva aproxima los puntos. Mientras que el primer tipo de spline es particularmente útil en procesos de digitalización de datos y especificación de trayectos para animación, el segundo es principalmente usado en herramientas de diseño para estructurar superficies de objetos. Condiciones de continuidad

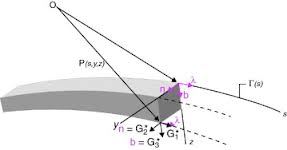
Al estar compuesta por varias partes de polinomios cúbicos, la suavidad de una spline puede especificarse imponiendo condiciones de continuidad entre secciones. Continuidad paramétrica Cn exige que las derivadas de grado n de las secciones polinomiales coincida. Continuidad geométrica Gn exige que la dirección y sentido de las derivadas de grado n coincida. Si bien la continuidad paramétrica normalmente es más fuerte que la geométrica, existen casos especiales (cuando la derivada vale 0) en que Gn no implica Cn.

Curvas de Hermite

La forma Hermite de un segmento de curva polinomial cúbica es determinada por los puntos extremos P1 y P2 y los vectores tangentes P1′ y P2′. Usando estos valores, podemos despejar las incógnitas Bi de la ecuación paramétrica (en este caso normalizada) y obtener:







3.3.5 Curvas y Superficies de Bezier

La Geometría Diferencial de Gauss trata del estudio de curvas y superficies, e incluso objetos de más dimensiones denominados variedades.

Básicamente, el método consiste en describir las curvas o superficies a estudiar con una función vectorial de unos parámetros, que hacen que un vector se mueva sobre dicha curva al variar el parámetro de forma local.

Hay que tener en cuenta que esto solo es necesario de forma local. Tal y como está expresado el enunciado, puede inducir a pensar que la Geometría Diferencial describe las superficies como una función vectorial de dos parámetros. Esto es falso, puesto que ha de definirse una función vectorial de dos parámetros sobre un abierto para cada punto de la superficie, pudiendo darse el caso en que distintos puntos deban ser representados por funciones distintas sobre abiertos distintos.

Otro matiz que debe hacerse a la anterior afirmación es el carácter diferenciable de estas funciones, que es lo que distinguiría el estudio de curvas, superficies y variedades que hace la Geometría Diferencial del que hace la Topología..